CHAPITRE 11 : POINTEURS ET FONCTIONS II #

Cours #

1242.1.11_Fonctions_II

Quiz #

Tableaux 2D #

Tableaux 2D statiques #

1ère et 2nde dimensions fixes et connues à la compilation #

#include <stdio.h>

// gcc error: variable-sized object may not be initialized
// const int N = 9;
// const int M = 10;
#define N 2
#define M 2

void init_static_2d_array_V1(int array[N][M], int nb_rows, int nb_cols);
void print_static_2d_array_V1(int array[N][M], int nb_rows, int nb_cols);

int main(void)
{  
  // Dimensions are known at compile time
  // => Static array
  // => Can be initialized
  int static_2d_array[N][M] = {0};
  init_static_2d_array_V1(static_2d_array, N, M);
  print_static_2d_array_V1(static_2d_array, N, M);

  return 0;
}

void init_static_2d_array_V1(int array[N][M], int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      array[i][j] = 10*i + j;
    }
  }
}

void print_static_2d_array_V1(int array[N][M], int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j)
    {
      printf("%d\t", array[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}

AVANTAGES :
Fonctionne avec les anciennes versions de C.

INCONVÉNIENTS :
Solution non-générique. Elle ne fonctionne que pour des tableaux 2D de taille N x M.

2nde dimension fixe et connue à la compilation #

#include <stdio.h>

// gcc error: variable-sized object may not be initialized
// const int N = 9;
// const int M = 10;
#define N 2
#define M 2

void init_static_2d_array_V2(int array[][M], int nb_rows, int nb_cols);
void print_static_2d_array_V2(int array[][M], int nb_rows, int nb_cols);

int main(void)
{  
  // Dimensions are known at compile time
  // => Static array
  // => Can be initialized
  int static_2d_array[N][M] = {0};

  init_static_2d_array_V2(static_2d_array, N, M);
  print_static_2d_array_V2(static_2d_array, N, M);

  return 0;
}

void init_static_2d_array_V2(int array[][M], int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      array[i][j] = 10*i + j;
    }
  }
}

void print_static_2d_array_V2(int array[][M], int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      printf("%d\t", array[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}

AVANTAGES :
Fonctionne avec les anciennes versions de C.

INCONVÉNIENTS :
Solution non-générique. Elle ne fonctionne que pour des tableaux 2D de taille * x M.

Utilisation de pointeurs #

#include <stdio.h>

// gcc error: variable-sized object may not be initialized
// const int N = 9;
// const int M = 10;
#define N 2
#define M 2

void init_static_2d_array_V3(int *array, int nb_rows, int nb_cols);
void print_static_2d_array_V3(int *array, int nb_rows, int nb_cols);

int main(void)
{  
  // Dimensions are known at compile time
  // => Static array
  // => Can be initialized
  int static_2d_array[N][M] = {0};

  // Cast is needed to cast from int (*)[M] to int *
  init_static_2d_array_V3((int*)static_2d_array, N, M);
  print_static_2d_array_V3((int*)static_2d_array, N, M);

  return 0;
}

void init_static_2d_array_V3(int *array, int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      *(array + i*nb_cols + j) = 10*i + j;
    }
  }
}

void print_static_2d_array_V3(int *array, int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      // printf("%d\t", *(array + i*nb_cols + j));
      // **OR**
      printf("%d\t", array[i*nb_cols + j]);
    }
    printf("\n");
  }
  printf("\n");
}

AVANTAGES :
Fonctionne avec les anciennes versions de C.
Solution générique.

INCONVÉNIENTS :
Solution plus complexe car on utilise des pointeurs.
Il faut caster le tableau au moment de l’appel aux fonctions.

[AVANCÉ] Utilisation de pointeurs avec formalisme tableau #

#include <stdio.h>

// gcc error: variable-sized object may not be initialized
// const int N = 9;
// const int M = 10;
#define N 2
#define M 2

void init_static_2d_array_V4(int *array, int nb_rows, int nb_cols);
void print_static_2d_array_V4(int *array, int nb_rows, int nb_cols);

int main(void)
{  
  // Dimensions are known at compile time
  // => Static array
  // => Can be initialized
  int static_2d_array[N][M] = {0};

  // Cast is needed to cast from int (*)[M] to int *
  init_static_2d_array_V4((int*)static_2d_array, N, M);
  print_static_2d_array_V4((int*)static_2d_array, N, M);

  return 0;
}

void init_static_2d_array_V4(int *array, int nb_rows, int nb_cols)
{
  int(*p_array)[nb_rows][nb_cols] = (int(*)[nb_rows][nb_cols])array;

  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      (*p_array)[i][j] = 10*i + j;
    }
  }
}

void print_static_2d_array_V4(int *array, int nb_rows, int nb_cols)
{
  int(*p_array)[nb_rows][nb_cols] = (int(*)[nb_rows][nb_cols])array;

  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      printf("%d\t", (*p_array)[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}

AVANTAGES :
Fonctionne avec les anciennes versions de C.
Solution générique.
On peut utiliser le formalisme tableau.

INCONVÉNIENTS :
Solution encore plus complexe car il faut faire des casts.
Il faut caster le tableau au moment de l’appel aux fonctions.

Tableaux 2D de taille variable (VLAs) #

Solution générique #

#include <stdio.h>

const int VLA_N = 3;
const int VLA_M = 3;

int main(void)
{  
  // gcc error: variable-sized object may not be initialized
  // Dimensions are known at runtime
  // => Variable Length Array (VLA)
  // => Cannot be initialized
  // int vla_2d_array[VLA_N][VLA_M] = {0};

  int vla_2d_array[VLA_N][VLA_M];

  init_vla_2d_array(VLA_N, VLA_M, vla_2d_array);
  print_vla_2d_array(VLA_N, VLA_M, vla_2d_array);

  return 0;
}

void init_vla_2d_array(int nb_rows, int nb_cols, int array[nb_rows][nb_cols])
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      array[i][j] = 10*i + j;
    }
  }
}

void print_vla_2d_array(int nb_rows, int nb_cols, int array[nb_rows][nb_cols])
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      printf("%d\t", array[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}

AVANTAGES :
Solution générique.
Solution intuitive et simple.

INCONVÉNIENTS :
C99 ou ultérieure uniquement.
Il faut passer les dimensions du tableau avant le tableau.

Tableaux 2D dynamiques #

#include <stdio.h>
#include <stdlib.h>

int **create_dynamic_2d_array(int nb_rows, int nb_cols);
void destroy_dynamic_2d_array(int **array, int nb_rows); // cols not needed here
void init_dynamic_2d_array(int **dynamic_array, int nb_rows, int nb_cols);
void print_dynamic_2d_array(int **dynamic_array, int nb_rows, int nb_cols);

int main(void)
{  
  int **dynamic_array = create_dynamic_2d_array(9, 5);
  init_dynamic_2d_array(dynamic_array, 9, 5);
  print_dynamic_2d_array(dynamic_array, 9, 5);
  destroy_dynamic_2d_array(dynamic_array, 9);

  return 0;
}

int **create_dynamic_2d_array(int nb_rows, int nb_cols)
{
  int **array = malloc(nb_rows*sizeof(int*));
  for (int i = 0; i < nb_rows; ++i)
  {
    array[i] = malloc(nb_cols*sizeof(int));
  }

  return array;
}

void destroy_dynamic_2d_array(int **array, int nb_rows)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    free(array[i]);
  }

  free(array);
  array = NULL;
}

void init_dynamic_2d_array(int **array, int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      // Warning
      // *(array +i*nb_cols + j) = 10*i + j; WONT work because array is a pointer to a pointer
      array[i][j] = 10*i + j;
    }
  }
}

void print_dynamic_2d_array(int **array, int nb_rows, int nb_cols)
{
  for (int i = 0; i < nb_rows; ++i)
  {
    for (int j = 0; j < nb_cols; ++j) 
    {
      printf("%d\t", array[i][j]);
    }
    printf("\n");
  }
  printf("\n");
}

AVANTAGES :
Fonctionne avec les anciennes versions de C.
Solution générique.
Meilleur gestion de la mémoire que les tableaux statiques.

INCONVÉNIENTS :
Solution plus compliquée car elle utilise l’allocation dynamique de mémoire ainsi que les pointeurs.

EXERCICES #

Exercice 1 [DÉPLACÉE] #

VOIR Chapitre 9, exercice 10.

Exercice 2 #

Écrire une fonction ch11_ex02_Reset() qui remet à zéro une valeur entière passée en argument. Écrire une fonction ch11_ex02_TestAndReset qui appelle la fonction ch11_ex02_Reset() si la valeur reçue (sous forme de pointeur) est différente de 0.

Exercice 3 #

Écrire une fonction void ch11_ex03_ResetPointer() qui met à NULL un pointeur d’entier passé en paramètre.

Exercice 4 #

Reprendre l’exercice 2 de la série 10, et « factoriser » le programme écrit en encapsulant le code dans les fonctions read_size(), allocate_array(), fill_array(), print_array(), free_array(). Le programme principal (main) prendra alors une forme concise et modulaire :

int main(void)
{
	int *ptr_tab = NULL;
	int N;
	N = read_size();
	ptr_tab = allocate_array(N);
	fill_array(ptr_tab, N);
	print_array(ptr_tab, N);
	printf("%p %d bytes\n", ptr_tab, (int)sizeof(ptr_tab));
	free_array(&ptr_tab);
	printf("%p %d bytes\n", ptr_tab, (int)sizeof(ptr_tab));
	// Note: the variable ptr_tab still exists here (4 bytes)

	return 0;
}

Exercice 5 #

a) Écrire un programme qui accepte un argument de type char à son lancement. Celui-ci déterminera la langue de l’utilisateur et affichera un message de salutations approprié.

b) Si la langue n’est pas supportée définir un code d’erreur et le renvoyer au système d’exploitation. Afficher un message informatif.

Exemples :

> .\Saluations.exe
Hello world!

> .\Saluations.exe e
Hello World!

> .\Saluations.exe F
Salut tout le monde!

> .\Saluations.exe d
Salu Tzame!

> .\Saluations.exe I
Ciao Mondo!

> .\Saluations.exe z
Langue non supportee, Achetez la version PREMIUM!

Exercice 6 #

Écrire une fonction compute_integral() qui calcule l’intégrale I d’une fonction f(x) quelconque définie entre deux bornes x=a et x=b :

\( I = \int_{a}^{b} f(x)dx \)

La fonction compute_integral() prendra en paramètre un pointeur sur la fonction dont on veut calculer l’intégrale (callback), et les valeurs réelles de a et b.

Le calcul de l’intégrale se fera selon une méthode simple d’accumulation de toutes les valeurs de la fonction de calcul entre les limites a et b. On subdivisera en 1000 tranches la fonction et cumuler les surfaces rectangulaires selon le principe suivant :

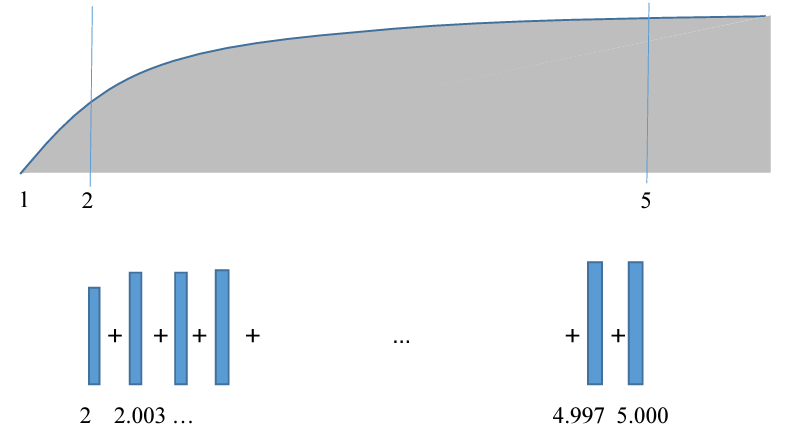
Exercice 7 #

Écrire une fonction ch11_ex07_EditArray() qui reçoit en paramètre un tableau d’entiers, sa taille ainsi qu’une fonction qui va modifier les éléments du tableau. Deux fonctions seront utilisées, ch11_ex07_Times2() et ch11_ex07_Times4() (voir plus bas). Ces fonctions seront appliquées à tous les éléments du tableau. Elles sont passées en arguments à la fonction ch11_ex07_EditArray() de 3 manières différentes :

La fonction elle-même
Un pointeur de fonction
Un élément d’un tableau de pointeurs de fonction.

Enfin, écrire une fonction ch11_ex07_FunctionsPointers() permettant de tester les 3 manières de passer une fonction en paramètre.

La fonction ch11_ex07_Times2() prend un entier en paramètre, le multiplie par 2, puis retourne le résultat.

La fonction ch11_ex07_Times4() prend un entier en paramètre, le multiplie par 4, puis retourne le résultat.

Exemples :

                          Initial array:     1     2     3     4
                            Function x2:     2     4     6     8
                            Function x4:     8    16    24    32 
                    Function pointer x2:    16    32    48    64
                    Function pointer x4:    64   128   192   256
                Function pointers array:   128   256   384   512
                Function pointers array:   512  1024  1536  2048

Squelette de la fonction ch11_ex07_FunctionsPointers() :

void ch11_ex07_FunctionsPointers(void)
{  
  int tab[] = {1, 2, 3, 4};
  int size = sizeof(tab) / sizeof(int);
  ch11_ex07_PrintArray("Initial array:", tab, size);

  // TODO: call ch11_ex07_EditArray() with functions directly
  ch11_ex07_PrintArray("Function x2:", tab, size);

  // TODO: call ch11_ex07_EditArray() with functions directly
  ch11_ex07_PrintArray("Function x4:", tab, size);

  // TODO: define a function pointer to ch11_ex07_Times2

  // TODO: call ch11_ex07_EditArray() with a function pointer
  ch11_ex07_PrintArray("Function pointer x2:", tab, size);

  // TODO: define a function pointer to ch11_ex07_Times4

  // TODO: call ch11_ex07_EditArray() with a function pointer
  ch11_ex07_PrintArray("Function pointer x4:", tab, size);

  // TODO: define an array containing 2 functions pointers

  for (int i = 0; i < 2; i++)
  {
    // TODO: call ch11_ex07_EditArray with elements of the defined functions pointers array
    ch11_ex07_PrintArray("Function pointers array:", tab, size);
  }
}

Fonction ch11_ex07_PrintArray() :

void ch11_ex07_PrintArray(const char *text, int t[], int n)
{
  printf("%40s ", text);
  for (int i = 0; i < n; i++)
  {
    printf("%5d ", t[i]);
  }
  printf("\n");
}

Exercice 8 #

Compléter l’exercice 3 de manière à pouvoir trier le tableau une fois dans l’ordre croissant et une fois dans l’ordre décroissant avec la fonction qsort() de la bibliothèque <stdlib.h>.

Description de la fonction `qsort()` #

Introduction #

La fonction qsort() implémente un algorithme de tri non spécifié qui permet de trier tout ou partie de n’importe quel tableau de données, du moment qu’il existe un critère de tri dans les données. Elle s’appuie sur une fonction utilisateur qui se charge d’exprimer le critère de tri.

Interface #

Le prototype de la fonction qsort() est :

void qsort(void *tableau, size_t nb_elem, size_t taille_elem, int (*compare) (void const *a, void const *b));

Paramètres :

void *tableau : adresse du 1er élément du tableau (pas constant) à trier
size_t nb_elem : nombre d’éléments du tableau à trier. Ne pas confondre avec sa taille.
size_t taille_elem : taille d’un élément du tableau (sizeof (*tab))
int (*compare) (void const *a, void const *b) : adresse de la fonction de comparaison (pointeur de fonction) à fournir. Cette fonction possède 2 paramètres void const *a et void const *b représentant l’adresse d’un des éléments du tableau en cours d’évaluation par l’algorithme.

La fonction compare() doit retourner un int avec la valeur suivante (tri croissant) :

= 0 si le critère de a est égal au critère de b
< 0 si le critère de a est inférieur au critère de b
> 0 si le critère de a est supérieur au critère de b

Comportement #

La fonction qsort() effectue le tri du tableau selon le critère indiqué. La valeur retournée par la fonction de comparaison permet à l’algorithme de prendre les décisions qui s’imposent. La fonction de comparaison reçoit l’adresse des 2 éléments en cours d’évaluation. Par l’intermédiaire de pointeurs locaux typés et initialisés avec ces paramètres, elle doit évaluer le critère de tri et retourner un int de la valeur résultant de l’évaluation. Pour un entier, une simple différence suffit. Pour une chaine, les fonctions strcmp(), strncmp() ont été conçues pour ça. Pour un réel, c’est plus délicat, car la notion d’égalité est soumise à l’appréciation d’un EPSILON qui dépend de la précision recherchée.